Acknowledgements: This article is based on the work of
Peter Sanders and
Roman Dementiev. You can find the full source code presented here in their
STXXL library (STL library for large data structures), Peter Sanders'
paper and the accompanying
source code.
Warning: If you are of sensitive nature either regarding
- computer science theory
- highly practical program optimization
then I recommend you to stop reading this article at once. You might faint or something. Maybe, however, you can get a
“bling” moment out of this article.
Do you remember
Mergesort from your introductory course in programming or computer science? An essential part of it is merging two already sorted lists into one as demonstrated in the animation below.
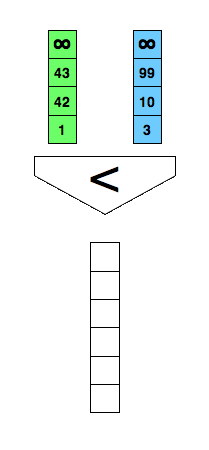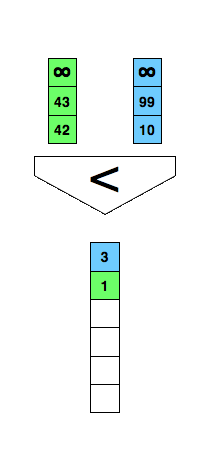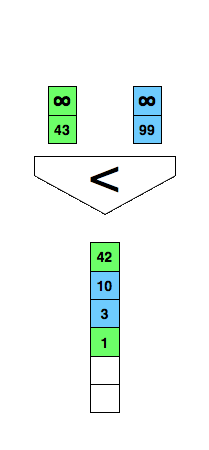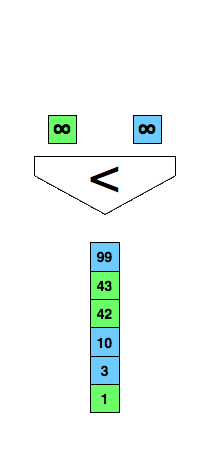
/* Merge two already sorted arrays where both are terminated
* by 0x0fff ffff which may not appear *inside* arrays.
*/
void merge2(int a[], int b[], int result[]) {
int i = 0, j = 0, k = 0;
while (true) {
if (a[i] <= b[j]) {
result[k] = a[i];
i += 1; k += 1;
} else {
result[k] = b[j];
j += 1; k += 1;
}
if (result[k] == 0x0fffffff) return;
}
}
If you are like me you do not think about Mergesort any more after understanding it and writing the exam it is relevant for. After all - people tell you that
Quicksort has the same average run time and is normally faster and in place. This is not true in the general case but I'll keep that for another article.
So, what is the deal about merging? If you complete your initial courses on algorithms and do not pursue algorithmics any further then chances are pretty good that you go ahead to things with more quickly visible and “tangible” results such as “enterprise” programs. But you shut your eyes to a pretty interesting part of computer science: Algorithmics.
Merging gets interesting if you deal with
I/O efficient algorithms: If you process data sets that do not fit your main memory any more then you will propably want to minimize I/O requests lest your shiny new Core 2 Duo processor will wait for your slow hard disk most of the time. Similar things have to be considered for the performance difference of your slow DRAM and the fast on CPU caches.
Sequence Heaps are a highly I/O efficient (and cache efficient for data sets that fit into main memory) data structure for maintaining priority queues.
Applications for priority queues include graph algorithms where you want to find the next largest node in your graph as fast as possible and graphs can get huge (think of all streets in Europe or North America, for example).
The data structure described by Sanders requires an efficient
R-way merger (where
R is less than or equal to 4 for practicable sizes). Building a two way merger was pretty simple and we could extend this to a 4 way merger:
/* Merge four already sorted arrays where both are terminated
* by 0x0fff ffff which may not appear *inside* arrays.
*/
void naive_merge4(int a[], int b[], int c[], int d[], int result[]) {
int i = 0, j = 0, k = 0, l = 0, m = 0;
while(true) {
if (a[i] <= b[j] && a[i] <= c[k] && a[i] <= d[l]) {
result[m] = a[i];
m += 1; i += 1;
} else if (b[j] <= a[i] && b[j] <= c[k] && b[j] <= d[l]) {
result[m] = b[j];
m += 1; j += 1;
} else if (c[k] <= a[i] && c[k] <= b[j] && c[k] <= d[l]) {
result[m] = c[k];
m += 1; k += 1;
} else { /* (d[l] <= a[i] && d[l] <= b[j] && d[l] <= c[k]) */
result[m] = d[l];
m += 1; l += 1;
}
if (result[m] == 0x0fffffff) return;
}
}
OK, so we are all fluffy and set now, aren't we? If all arrays have the same length
n then our
naive_merge4 will run in
O(n) and we cannot expect a better asymptotic runtime, right?
We will not be able to improve on the asymptotic runtime since we have to look at least once at each element but each of our if statements has
three comparisons! We have to do nine comparisons each time
d contains the smallest element!
Can we do better? We could use the comparison demonstrated in the following figure and reduce the comparisons to three in every case.
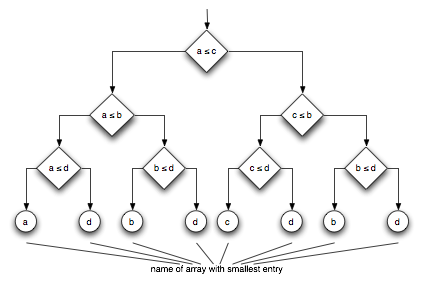
Can we do even better? The answer is: Yes, we can - using Sander's code for four way merging:
template
void merge4_iterator(
InputIterator & from0,
InputIterator & from1,
InputIterator & from2,
InputIterator & from3,
OutputIterator to, int_type sz, Cmp_ cmp)
{
OutputIterator done = to + sz;
#define StartMerge4(a, b, c, d)\
if ( (!cmp(*from##a ,*from##b )) && (!cmp(*from##b ,*from##c )) \
&& (!cmp(*from##c ,*from##d )) )\
goto s ## a ## b ## c ## d ;
// b>a c>b d>c
// a<b b<c c<d
// a<=b b<=c c<=d
// !(a>b) !(b>c) !(c>d)
StartMerge4(0, 1, 2, 3);
// [...] call StartMerge4 for every permutation of 0, 1, 2, 3
#define Merge4Case(a, b, c, d)\
s ## a ## b ## c ## d:\
if (to == done) goto finish;\
*to = *from ## a ;\
++to;\
++from ## a ;\
if (cmp(*from ## c , *from ## a))\
{\
if (cmp(*from ## b, *from ## a )) \
goto s ## a ## b ## c ## d; \
else \
goto s ## b ## a ## c ## d; \
}\
else \
{\
if (cmp(*from ## d, *from ## a))\
goto s ## b ## c ## a ## d; \
else \
goto s ## b ## c ## d ## a; \
}
Merge4Case(0, 1, 2, 3);
// [...] call Merge4Case for every permutation of 0, 1, 2, 3
finish:
return;
}
So, what's happening here? The macro
Merge4Case generates the code for a specific ordering of the input streams
from0, ...,
from3. For each ordering, the next case can be found using only two comparisons (see the figure below). The macro
StartMerge4 merely gets us started by jumping to the appropriate case.
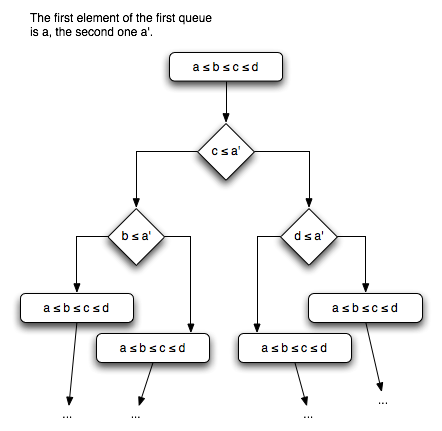
We have to do some work for initialization but after that we only have to do
only two comparisons for each merge step! The instruction pointer (i.e. the current point of execution in the code) encodes the ordering of the input streams' ordering.
Of course, there is a tradeoff: While
naive_merge4 is only 20 lines long, the code
merge4_iterator expands to much more than 200 lines. Of course, the native code does not correlate directly with the number of lines but the optimized variant will make the compiler create much more code than the naive merge method.
The code for the optimized 4 way merger fits into the instruction cache and the tradeoff makes sense. However, we have to keep in mind that the code generated is dependent on the number of permutation of input streams. Thus, it is in
O(R!). While
4! is only
24 a calculator or pen and paper give us
40'320 for
8!. I guess the code generated for an 8 way merger might not quite fit into the L1 instruction cache of the common CPUs out there (
Wikipedia tells us that the Itanium 2 has a 16KB L1 instruction cache and a 256KB L2 cache that is used for both instructions and data).
So, what can we learn from this?
- There are very elegant and powerful uses of the C preprocessor and the otherwise harmful GOTO.
- People at universities can write very pragmatic and efficient code.
- Algorithmics can be interesting (hopefully).
Updates
- Changed < to <= in the merge algorithms where it was wrong.

 Can we do even better? The answer is: Yes, we can - using Sander's code for four way merging:
Can we do even better? The answer is: Yes, we can - using Sander's code for four way merging:
 We have to do some work for initialization but after that we only have to do only two comparisons for each merge step! The instruction pointer (i.e. the current point of execution in the code) encodes the ordering of the input streams' ordering.
Of course, there is a tradeoff: While naive_merge4 is only 20 lines long, the code merge4_iterator expands to much more than 200 lines. Of course, the native code does not correlate directly with the number of lines but the optimized variant will make the compiler create much more code than the naive merge method.
The code for the optimized 4 way merger fits into the instruction cache and the tradeoff makes sense. However, we have to keep in mind that the code generated is dependent on the number of permutation of input streams. Thus, it is in O(R!). While 4! is only 24 a calculator or pen and paper give us 40'320 for 8!. I guess the code generated for an 8 way merger might not quite fit into the L1 instruction cache of the common CPUs out there (Wikipedia tells us that the Itanium 2 has a 16KB L1 instruction cache and a 256KB L2 cache that is used for both instructions and data).
So, what can we learn from this?
We have to do some work for initialization but after that we only have to do only two comparisons for each merge step! The instruction pointer (i.e. the current point of execution in the code) encodes the ordering of the input streams' ordering.
Of course, there is a tradeoff: While naive_merge4 is only 20 lines long, the code merge4_iterator expands to much more than 200 lines. Of course, the native code does not correlate directly with the number of lines but the optimized variant will make the compiler create much more code than the naive merge method.
The code for the optimized 4 way merger fits into the instruction cache and the tradeoff makes sense. However, we have to keep in mind that the code generated is dependent on the number of permutation of input streams. Thus, it is in O(R!). While 4! is only 24 a calculator or pen and paper give us 40'320 for 8!. I guess the code generated for an 8 way merger might not quite fit into the L1 instruction cache of the common CPUs out there (Wikipedia tells us that the Itanium 2 has a 16KB L1 instruction cache and a 256KB L2 cache that is used for both instructions and data).
So, what can we learn from this?

11 comments:
That 'naive_merge4' function is incorrect. Consider what happens if the four compared values are 1, 1, 2, and 3 -- the algorithm will pick 3 since none of the first three items are strictly less than all the others. I think replacing "<" with "<=" in those comparisons would fix that.
The case for 4 arrays doesn't need to be that complicated because you can reuse the same method - result[] is itself a sorted array and can be used as input.
Here's an example:
/* Merge four already sorted arrays where both are terminated
* by 0x0fff ffff which may not appear *inside* arrays.
*/
void merge4(int a[], int b[], int c[], int d[], int result[]) {
int i = 0, j = 0, k = 0, l = 0, m = 0;
int ab, cd;
while (true) {
if (a[i] < b[j]) {
ab = a[i];
i += 1;
} else {
ab = b[j];
j += 1;
}
if (c[l] < d[m]) {
cd = c[i];
l += 1;
} else {
cd = d[j];
m += 1;
}
if (ab < cd) {
result[k] = ab;
k += 1;
} else {
result[k] = cd;
k += 1;
}
if (result[k] == 0x0fffffff) return;
}
}
this was (a,b) => ab; (c,d) => cd; (ab,cd) => result
similarly, for ex. 7 arrays a[],b[],c[],d[],e[],f[],g[]
(a,b) => ab; (c,d) => cd; (e,f) =ef;
(ab,cd) => abcd;
(ef,g) => efg;
(abcd,efg) => result;
for n arrays code size is roughly 2*n and temp variables n/2 (if, in the 7 arrays example we re-use ab instead of another variable, abcd)
and yes, Algorithmics rock!
Anonymous #1: Thanks for the corrections. I fixed this. There is no excuse for incorrect sample code but to quote Knuth: "Be careful about using the following code -- I've only proven that it works, I haven't tested it."
Anonymous #2: This looks interesting. However, I can see two issues:
* I guess you meant "cd = c[l]" instead of "cd = c[i]" and "cd = c[m]" instead of "cd = d[j]".
* Are you sure that your algorithm works correctly? To me, it seems that you always skip the smallest entry of all sorted sequences and only store it once. If I understand your algorithm correctly then it is wrong. Please correct me if I am wrong.
There's another problem with the merge2() function. When you check the value of result[k] you have already incremented k so it is not the last value assigned. You need to check result[k-1]!
The last image seems wrong, and/or a bit hard to understand.
In the second image, it looks like when a comparison holds (e.g. a < c == true) you branch left, otherwise you branch right.
In the last image you seem to branch right instead, but it's a bit hard to tell because the bottom group of boxes have an incorrect text in them (I think).
If I understand the algorithm, you get into a start state where the four streams are sorted in ascending order of their head element. Then you pop the head element off the "first" stream, and re-sort the streams by figuring out where to put the "first" stream based on its (new) head element, and do this over and over until you're out of elements.
So your image (turned 90 degrees counter-clockwise) should look something like:
[b <= c <= d <= a']
(a' <= d)
[b <= c <= a' <= d]
(a' <= c)
[b <= a' <= c <= d]
(a' <= b)
[a' <= b <= c <= d]
Here is a much simpler way and it only needs two compares per merge. (it was based of anonymous-2 code)
void merge4(int a[], int b[], int c[], int d[], int result[])
{
int ab = *a < *b ? *a++ : *b++;
int cd = *c < *d ? *c++ : *d++;
do
{
if(ab < cd)
{
*result = ab;
ab = *a < *b ? *a++ : *b++;
}
else
{
*result = cd;
cd = *c < *d ? *c++ : *d++;
}
}
while(*result++ != 0xffFFffFF);
}
Why not use a min heap?
john: Thank you for comment, it is indeed simpler and also only uses 2 comparisons - thus in the RAM model, the costs are the same.
However - I did not point that out clearly in the article - you have to look at the input streams two times for every iteration and this might be slow.
Actually, your implementation is a in-register Tournament Tree that I will write about in a later article.
anonymous: Min Heaps are highly cache inefficient. I will write about this in the bitwiese blog, too.
Instead of using preprocessor define statements, I would recommend using C++ templates that will do the loop unrolling for you in compile time and won't look so ugly (yes I accept that even templates look a little bit ugly)
http://www.ddj.com/cpp/184401634
Can this algorithm be adapter to 3-way or 2-way merging as well? I'm trying to think of some ways that it can.
This one is good. keep up the good work!.. wärmerückgewinnung industrie
Post a Comment