Acknowledgement (2011-11-21): You should search Google for your blog titles before hitting "publish". When I wrote this article some years back, "hitting the memory wall" was just a term I had read some time earlier and internalized for myself as a standing term, like folklore. This was wrong. There is a paper from 1995 by WA Wulf and SA McKee with the same title: Hitting the memory wall that I was not aware of to this day. Thanks to sam in the comments for pointing this out. Sorry, for being late with the acknowledgement.
You have always ignored the internals of CPU properties like the number of registers, the exact format of CPU words, the precise format of intructions and of course the cache. I know you have (well, let's say I am sure about 99% of you out there). I ignored this for a pretty long time, too, when programming (although I was lucky enough to be forced to learn about the general principles at university).
And it has always been enough for you, right? Your enterprisy Java programs ran nicely, your beautiful literal Haskell programs zipped smoothly along and your Ruby and Python scripts ran with whatever speed the interpreter made possible. Your C(++) programs ran well, too, didn't they?
At least they did for me (ignoring bugs) - until now. I ignored the CPU internals, kept to common programmer's sense and best practice. I made sure my sorting algorithms ran in O(n · log(n)), searching ran in O(log n) and generally made sure that all algorithms algorithms were in polynomial time and the constants in big-O notation were small.
I thought I was happy and no problem would occur to me. And so you might think. Think again.
Ready, set, go...
I was working on parallelizing Counting Sort, a simple integer sorting algorithm that runs in linear time and needs O(n) additional space.
The algorithm is given an array of integers in the range of [0, max_key] and then works as follows:
- For each integer from 0 to max_key, count the number of occurences in the input array.
- Then, determine for each of these integers, where the first one will be written to in the sorted array.
- Third, copy the elements from the input array into a buffer array at the right positions.
- At last, copy the elements from the buffer back into input array.
Note that the algorithm is stable, i.e. the order within the elements with the same keys is preserved. This property is important for its application in the DC3 algorithm for linear time Suffix Array construction.
1 /* Use the Counting Sort algorithm to sort the range
2 * [arr, arr + n). The entries must be in the range of
3 * [0, max_key]. */
4 static void counting_sort(int* arr, int n, int max_key)
5 {
6 // counter array
7 int* c = new int[K + 1];
8 // reset counters
9 for (int i = 0; i <= K; i++) c[i] = 0;
10 // count occurences
11 for (int i = 0; i < n; i++) c[arr[i]]++;
12
13 // compute exclusive prefix sums
14 for (int i = 0, sum = 0; i <= max_key; i++)
15 {
16 int t = c[i]; c[i] = sum; sum += t;
17 }
18
19 // copy elements sorted into buffer
20 int *buffer = new int[end - begin];
21 for (int i = 0; i < n; i++)
22 buffer[c[arr[i]]++] = arr[i];
23
24 // copy elements back into input
25 for (int i = 0; i < n; i++)
26 arr[i] = buffer[i];
27
28 // copy elements back
29 delete [] buffer;
30 delete [] c;
31 }
Also note that we copy back the elements from the input instead of simply filling up the result array with the keys we determined earlier. The reason for this is that the input array could be an array of objects which are then sorted by a certain integer property/key.
...and crash!
So, where is the problem? Counting Sort! One of the simplest algorithms there is. Taught in undergraduate courses or in school! Can it get simpler than that? Where can the problem be?
I wanted to parallelize the DC3 algorithm using the shared memory with OpenMP. DC3 needs a linear time integer sorter to run in linear time and the reference implementation uses counting sort for it.
So I threw in some parallel instructions: Line 14-16 were executed for each thread, i.e. every thread got an equally (plus minus one) sized part of the input array and counted the occurences. Afterwards, the threads were terminated and the master thread calculated the "global prefix sums" so all threads got the right positions to write to. Then, lines 21-22 were parallelized again.
The parallelelized code can be found here.
OK, so far - since the sequential work is reduced to memory allocation and the global prefix sum calculation (aka rank calculation) involves very few additions there should not be a problem, right? (Let us ignore the copy-back step for this article.)
So I compiled the source on our Dual Xeon (each with 2 cores) machine with GCC 4.2 and level 3 optimization and ran some benchmarks. The maximum key was set to 127 (i.e. we could sort ASCII strings), the array size set to 16M (i.e. 64GB of data since ints are 4 bytes long on the architecture, filled with random integers) and the number of threads was varied from 1 to 4. The results are shown below (the line numbers correspond to the sequential code not the parallel one):
| no. of threads | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| line 14-17 | 30.20 ms | 19.99 ms | 29.74 ms | 23.88 ms |
| lines 21-22 | 100.92 ms | 59.61 ms | 56.41 ms | 55.78 ms |
So, we get a speedup of about 1.5 with two threads but afterwards, there is no speedup at all. We should expect a speedup of n with n processors in these two parts since these sections were completely parallelized.
So, what the heck is happening there?
The von Neumann Bottleneck
It's the von Neumann Bottleneck, baby! Today's SMP (Shared Memory Processing) systems are still built similar to the von Neumann machine. You were propably taught about it if you have a computer science background:
- The main memory is accessible via random access and stores machine words.
- The bus connects main memory, processor, peripherical devices. Only one connected entity can use the bus at any given time.
- The processor loads data and instructions from the main memory and executes it.
- There are peripherical devices for input and output (HDD, keyboard etc.)
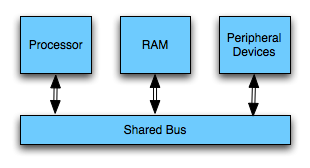
Today's computers do not work directly on the main memory, however, but normally on registers which can be accessed in one cycle. Read and write access to the main memory are cached in a cache hierarchy. The specs of the caches on the given machine were measured to be as follows:
| - | L1 Cache | L2 Cache | Main Memory |
|---|---|---|---|
| size | 32 KiB | 4 MiB | 8 GiB |
| latency [cycles] | 3 cycles | 9 cycles | 133 cycles |
| latency [time] | 1.28 ns | 3.94 ns | 56.95 ns |
Additionally, the memory bus bandwidth in the system is 6.4 GB/s (however, as usual with bandwidth you will not be able to actually transfer more than half of that data per second in a real system).
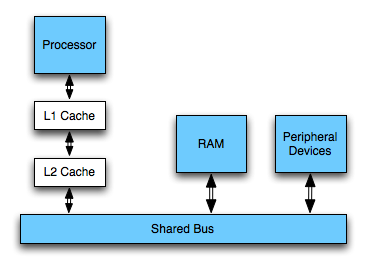
So let us see if we can explain the behaviour with the knowledge about the architecture and these numbers in mind.
Lines 14-17 are executed 224 times in total and because ints are 4 bytes wide, this makes 226 bytes = 64 MiB transferred from memory if we only consider arr[] - c[] is small enough to fit into the processor's cache all the time (even one copy for each core).
With one thread (i.e. one processor working), 64 MiB get read in 30 ms which means that 2.133 GiB/s were read. With two threads working, the 64 MiB get read in roughly 20ms which manes that 3.2 GiB/s were read - the memory bus is saturated, our algorithm gets memory I/O bound and has to wait for the slow SD-RAM.
A Strange Phenomenon
Now, let us try to transfer that calculation to lines 21-22 - it should be pretty easy now. Again, we can assume that c[] can be kept in the level 1 cache all the time. This leaves reading arr[] and writing to buffer[]. Note that buffer[] is more or less accessed randomly (depending on the order of the values in arr[]). However, there are only 127 positions in buffer that are written to (limited by the size of c[]) and thus we can keep these positions of buffer[] in the L2 cache.
We would expect lines 21-22 to take twice the time than lines 14-17 because there are twice as much memory accesses. However, it takes thrice the time with two threads where we would expect the bus saturation. It gets even a bit faster with more threds although we would expect the bus to be saturated already! What is happening?
The image of modern computers we drew above was not really exact: Modern operating systems use virtual memory with paging to protect applications from each other and the kernel from user land:
Programs use virtual addresses to address their variables and these virtual addresses have to be translated into physical addresses. The data in the cache is addressed physically so access of main memory requires a resolution of a virtual address into a physical address. The addressing is done page wise, e.g. in chunks of 4 KiB. Each of these pages has a virtual base address which has to be mapped to its physical address (the place the page resides in RAM is called page frame).
The operating system has a table for each process that has the mapping from virtual page addresses to physical ones. This table resides in memory, too, and has to be accessed for each memory access. Parts of these tables are kept in a special cache: The so called Translation Lookaside Buffer (TLB). The TLB of the system is again separated into two levels, the faster one is approximately as fast as the registers, the slower one as fast as the L1 cache.
Let us explain our results with these numbers.
Since the page size of the system is 4KiB, we only have to look at the page table every 1024th memory access in lines 14-17. This very few times and we can neglect the access times since they are few and fast (since the L1 TLB is hit).
In lines 25-26, we transfer 128MiB in and out of the RAM. This should take us about 40ms but the lines take use 60ms. However, since access is almost random, we expect to look at the L2 TLB almost every time we want to access buffer[]. This means looking at it 224 times with 1.28ns each. This simplified calculation yields 21ms for the TLB accesses which seems right considered that we will hit the L1 TLB some times, too.
Whee, I do not know about you, but I would like to see a summary of all this to wrap my mind around it properly.
Summary
We examined the parallelization of counting sort, a simple linear time sorting algorithm. The algorithm could be parallelized well but the parallel parts did not yield the expected linear speedup. We considered current, modern computer architectures and could explained our experimental results with the specs of the machine we used and the knowledge of the architecture.
Note, ladies and gentlemen that we are crossing the border between algorithmics and system architecture here: Sometimes, actually implemented algorithms behave different from theoretical results (which indicated a lineare speedup).
So, what's next? We could try to kick our "slow" sorting algorithm into the virtual nirvana and replace it by another one. But which one should we choose? Counting sort needs exactly 4 · n + O(k) operations for an array with the length of n containing values from 0 to k. Any comparison based algorithm like Quicksort would need much more operations and parallelizing them comes at a pretty high overhead. Bucketsort exhibits the same non-locality when copying back elements and Radixsort needs another stable sorting algorithm like counting sort internally. If you, dear reader, know of a better linear sorting algorithm then please let me know since it would solve a problem for me.
We could use a NUMA machine where each processor has its own memory bus and memory. After splitting the input array, each processor could sort its part in its own memory. However, the final result composition would be slower since access to other processor's memory is slow and we have to go through one single bottlenecky bus again.
I hope you had as much fun reading this article as I had analyzing the algorithm and writing the article.
We are looking forward to your comments.
Updates
- I think that I have not made it clear enough above that the algorithm actually is cache efficient. Everwhere, memory is accessed, it is only accessed ones and in streams (every entry of c points to a part of buffer and this can be considered a stream). Each of these streams is read/written sequentially. This seems to have been hidden by the description of modern computers' architecture above.

9 comments:
First, regarding your code snippet, you have a few minor errors that presumably came when you simplified it for posting.
For max_key, you use K, which is undefined.
You call delete on the buffer, which you've placed on the stack.
As well, readability is a problem, since the code lines get broken up.
Do you know if the affinity of your threads is working out correctly -- i.e. if the threads are actually running on different cores? If not, your performance would obviously get nailed.
In terms of speed, I would use a memset for initializing the (int) arrays, but that may just be me.
I've actually seen an algorithm that computes the running total (also called scan) well in parallel. If you look for GPU programming and scans, you should find it. I don't know if it would change anything in your case.
If memory bandwidth really is the problem, I think where you want to look is your buffer filling and copying. From looking at your real code, I realize you're actually copying objects, so there's a lot of memory shifting. Does it have to be in-place? Could you provide a sorted array of indices, and use those later?
You also compute the hash twice (and only check it after you've used it!). I think you might benefit by setting up a separate table with just the smaller hashes in them (smaller == happier cache!), and sorting a set of indices based on that.
Another question (that again only works on the constant, not the big O of your sort, but that's optimal anyway) -- why don't you actually iterate your iterator, rather than offsetting from begin? Since you're doing the index ranges of the parallel loops yourself, this should be fine. It's a minor change that should be easy to determine whether it speeds things up.
As an aside, out of principle I would be skeptical of the timing values you've traced to individual lines.
As another aside, I would also be curious as to how much gain you get when you using 'plain old data' types, and then use bulk memory functions (i.e. memcopy, no destructor/delete calls). I think the gain would not be trivial.
To sum things up, I would use simple C-style functions where possible, and sort on an array of indices of the pre-computed hashes.
(One final question, in your parallel code, where you're filling the buffer, you have the line buffer[c[hash(begin[i]]++] = begin[i]. Do you really want the '++' in there? Am I missing something?
For an even more staggering demonstration of theory diverging from reality, check out this blog entry about cache bounces (also known as "false sharing"). If multiple processors are simultaneously writing to the same cache line, performance can degrade by 1700%, according to the experimental results of this blogger!
Hi, Ben.
Thanks for finding the K in the source code - I did not replace it by the more verbose max_key in this place and yes, the buffer should be allocated on the heap. I also reformatted the code a bit so it should fit into the left column now.
The affinity of the threads seems to work since the processor usage goes to 170/180% which would fit with two threads already saturating the memory bandwidth.
Initializing the counter array could be done with memset but it does not be the actual bottleneck since max_key will be small (< 1000) in any case.
The running total problem you mention is known as "computing prefix sums" to me. The problem is commonly found in text books since they can be solved via the common divide and conquer algorithm. I do not think that this can apply here. Common divide and conquer algorithms like Mergesort and Quicksort can be parallelized but the Parallel Quicksort implementation I compared my Counting Sort against was slower by a factor 10 in the program I used it.
Regarding the speed of copying: Since I tested the parallel algorithm with int* as the RandomIterator, I would guess that the compiler simply copies ints which is fast.
Regarding the hash: I tested the algorithm with a simple identity functor which should have been optimized away by the compiler so I do not think that this is the problem with my benchmark.
I will try out whether using iterators instead offsets is faster although I remember faintly having heard that arrays are normally faster than working directly with pointers (which the iterators are since I used int* in my experiments).
Regarding having the timing traced to lines: I simply put timers around them and ran the algorithm with sufficiently large inputs. I do not think that there is a much better way to perform benchmarks.
As an aside, out of principle I would be skeptical of the timing values you've traced to individual lines.
Yes, in the parallel code, the ++ is intentional. The c[i] defines the position in buffer of the next element with the (hash) value i to be written to. After setting the current one, we have to increment this position.
Hi, Josh.
Thanks for mentioning this here. The issue was known to me and looking at my code, I guess I barely escape this problem because the counter arrays are large enough and have a power of two as their size (in my tests).
You might find this interesting: http://www.brics.dk/~gerth/Papers/alcomft-tr-03-101.ps.gz
You just need to run the threads one after the other. That way, each one will have full access to the processor cache. Let's know if that works.
UPDATE: Oops, won't work. A different algorithm is needed.
So why do you think it's OK to plagiarize my title w/o so much as an offhand reference? Seriously? Not cool. Way not cool.
@sam: Thank you for pointing out an origin for the term. I put up an acknowledgement at the top.
I reject the allegation of conscious plagerization, though!
I was not aware of your paper and am seeing it the first time. The discrepancy between memory and processor speed was pointed out so often during my years in school and I internalized "the memory wall" earlier such that I was not aware of duplicating your title.
I can see that you are an expert at your field! I am launching a website soon, and your information will be very useful for me.. Thanks for all your help and wishing you all the success in your business. wärmerückgewinnung industrie
Post a Comment